Description
Let 𝐴 be the abelian group given by 𝐴=𝑍3𝑁 where 𝑁 is the submodule of 𝑍3 generated by
{(-4,2,6),(-6,2,6),(7,4,15)}. If
𝑅=([-4,-6,7],[2,2,4],[6,6,15]),𝑥=([1,0,0],[6,1,2],[21,3,7]),𝑌=([0,3,-1],[1,-2,3],[1,0,2])
then
𝑥-1𝑅𝑌=([1,0,0],[0,2,0],[0,0,6]).
(i) Find a basis {𝑏1,𝑏2,𝑏3} of 𝑍3 such that {𝑑1𝑏1,𝑑2𝑏2,𝑑3𝑏3} generates 𝑁.
(ii) Find elements uinA and vinA that generate A and are such that 2𝑢=0 and 6𝑣=0.

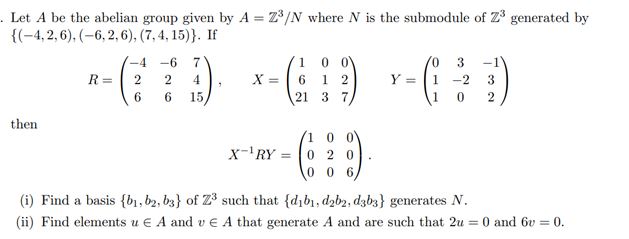

Reviews
There are no reviews yet.