Description
Suppose players A and 𝐵 have a coin tossing game going on-a fair coin is tossed and the player predicting the toss correctly wins $1 from the other player. Suppose the game goes on until one player has no money (is ruined). Complete parts (a) through (d) below.
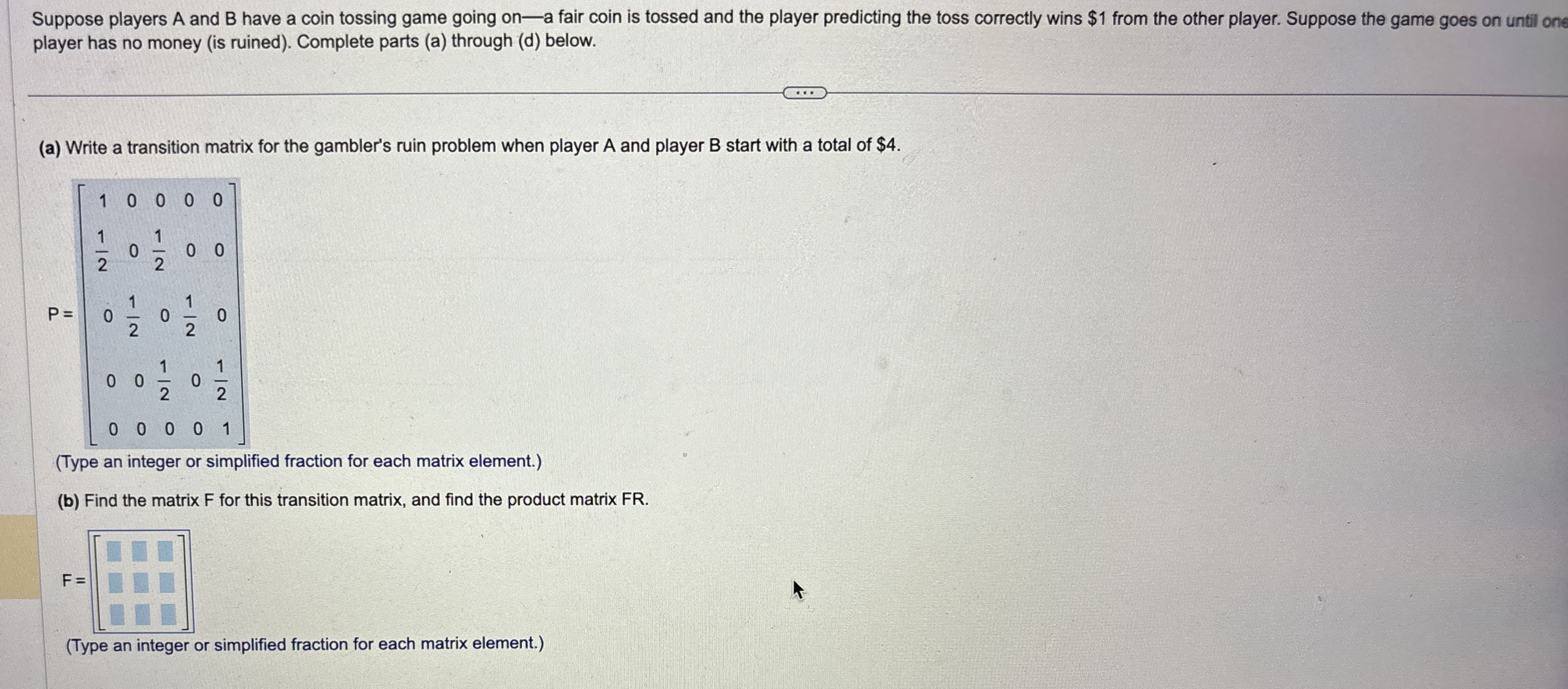
(a) Write a transition matrix for the gambler’s ruin problem when player A and player 𝐵 start with a total of $4.
𝑃=[1000012012000120120001201200001]
(Type an integer or simplified fraction for each matrix element.)
(b) Find the matrix 𝐹 for this transition matrix, and find the product matrix FR.
(Type an integer or simplified fraction for each matrix element.)


Reviews
There are no reviews yet.