Description
use vis-viva and calculate a:1. v22-μr=-μ2a
2. T=2πa3μ
3. define time step: Δt=T100
4. use vec(r)0 and vec(v)0 and ΔT to compute f,g and f˙,g˙
5. use equation vec(r)(t)=fvec(r)0+gvec(v)0 and vec(v)(t)=vec(r)˙=fr0˙+g0˙vec(v)0 to compute vec(r)1 and vec(v)1
6. validate your computed vec(r)1 and vec(v)1 in vis-visa equation
(hint:you must come up with same a value)
given:
μ=398600.435
vec(r)(km)
vec(v)(kms)
time = seconds
vec(r)0=7200hat(i)-800hat(ȷ)+350hat(k)
vec(v)0=0.2hat(i)+8.1hat(ȷ)-0.3hat(k)
Taylor’s Series Expansion
f=1-(μ2r03)Δt2+μ2(vec(r)0*vec(v)0r0s)Δt3
g=Δt-(16)(μr03)Δt3
f˙=ddt(f)
g˙=ddt(g)
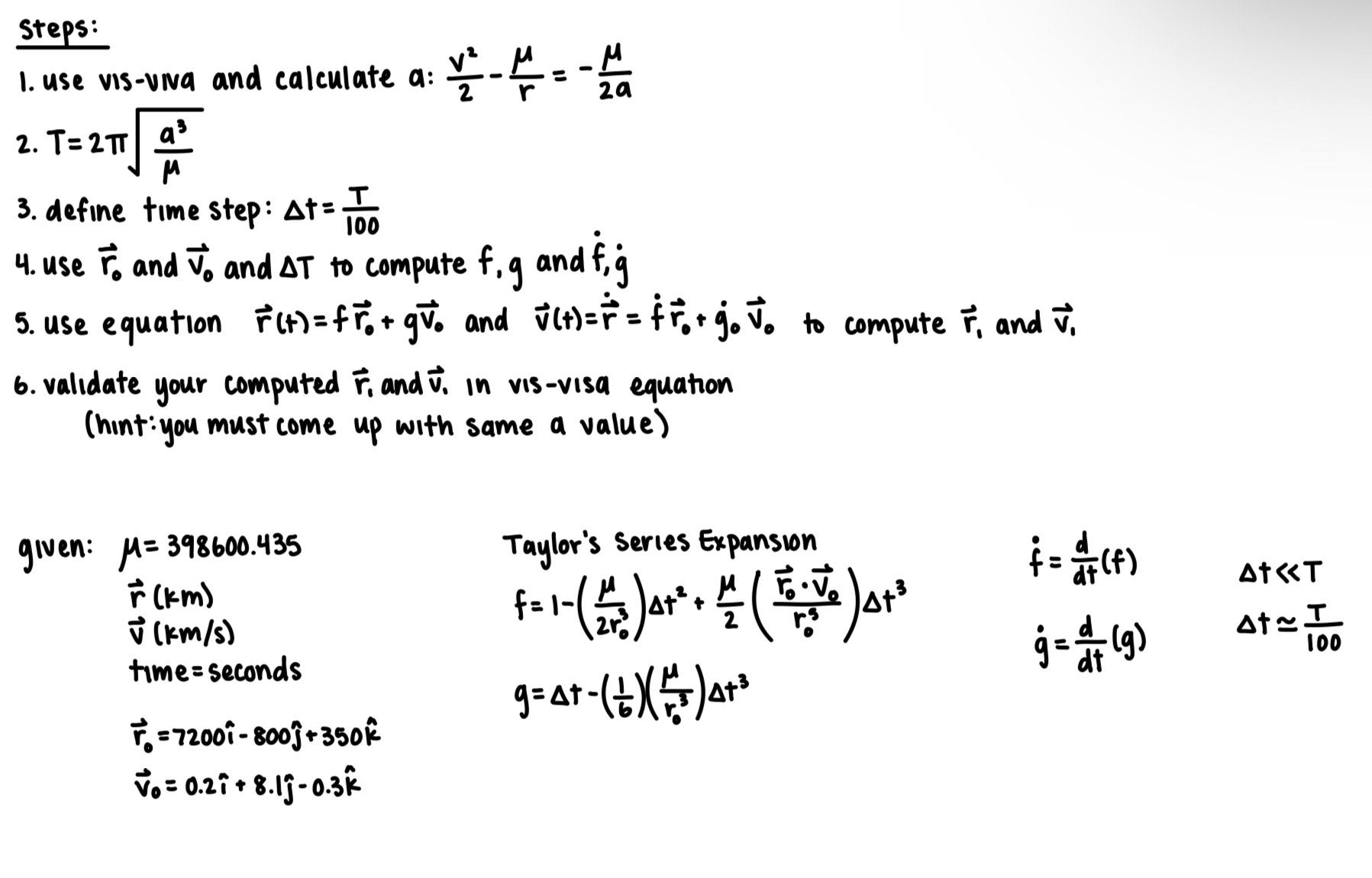



Reviews
There are no reviews yet.